Найти координаты фокусов эллипса онлайн калькулятор. Кривые второго порядка. Эллипс
Определение. Эллипсом называется геометрическое место точек плоскости, сумма расстояний каждой из которых от двух данных точек этой плоскости, называемых фокусами, есть постоянная величина (при условии, что эта величина больше расстояния между фокусами).
Обозначим фокусы через расстояние между ними - через , а постоянную величину, равную сумме расстояний от каждой точки эллипса до фокусов, через (по условию ).
Построим декартову систему координат так, чтобы фокусы оказались на оси абсцисс, а начало координат совпало с серединой отрезка (рис. 44). Тогда фокусы будут иметь следующие координаты: левый фокус и правый фокус . Выведем уравнение эллипса в выбранной нами системе координат. С этой целью рассмотрим произвольную точку эллипса. По определению эллипса сумма расстояний от этой точки до фокусов равна :
![]()
Пользуясь формулой для расстояния между двумя точками, получим следовательно,
Для упрощения этого уравнения запишем его в форме
Возведя затем обе части уравнения в квадрат, получим
или, после очевидных упрощений:
Теперь опять возводим обе части уравнения в квадрат, после чего будем иметь:
или, после тождественных преобразований:
Так как согласно условию в определении эллипса , то - число положительное. Введем обозначение
Тогда уравнение примет следующий вид:
![]()
По определению эллипса координаты любой его точки удовлетворяют уравнению (26). Но уравнение (29) является следствием уравнения (26). Следовательно, ему также удовлетворяют координаты любой точки эллипса.
Можно показать, что координаты точек, не лежащих на эллипсе, уравнению (29) не удовлетворяют. Таким образом, уравнение (29) есть уравнение эллипса. Оно называется каноническим уравнением эллипса.
Установим форму эллипса, пользуясь его каноническим уравнением.
Прежде всего обратим внимание на то, что это уравнение содержит только четные степени х и у. Это значит, что если какая-нибудь точка принадлежит эллипсу, то ему принадлежат также точка , симметричная с точкой относительно оси абсцисс, и точка симметричная с точкой относительно оси ординат. Таким образом, эллипс имеет две взаимно перпендикулярные оси симметрии, которые в выбранной нами системе координат совпадают с координатными осями. Оси симметрии эллипса мы в дальнейшем будем называть осями эллипса, а точку их пересечения - центром эллипса. Та ось, на которой расположены фокусы эллипса (в данном случае ось абсцисс), называется фокальной осью.
Определим форму эллипса сначала в I четверти. Для зтого разрешим уравнение (28) относительно у:
![]()
Очевидно, что здесь , так как у при принимает мнимые значения. При возрастании от 0 до а у уменьшается от b до 0. Частью эллипса, лежащей в I четверти, будет дуга, ограниченная точками В (0; b) и лежащими на осях координат (рис. 45). Воспользовавшись теперь симметрией эллипса, приходим к заключению, что эллипс имеет форму, изображенную на рис. 45.

Точки пересечения эллипса с осями называются вершинами эллипса. Из симметрии эллипса следует, что, кроме вершин , эллипс имеет еще две вершины (см. рис. 45).
Отрезки и соединяющие противоположные вершины эллипса, а также их длины , называются соответственно большой и малой осями эллипса. Числа а и b называются соответственно большой и малой полуосями эллипса.
Отношение половины расстояния между фокусами к большой полуоси эллипса называется эксцентриситетом эллипса и обозначается обычно буквой :
Так как , то эксцентриситет эллипса меньше единицы: Эксцентриситет характеризует форму эллипса. Действительно, из формулы (28) следует, Отсюда видно, что чем меньше эксцентриситет эллипса, тем меньше его малая полуось b отличается от большой полуоси а, т. е. тем меньше вытянут эллипс (вдоль фокальной оси).
В предельном случае при получится окружность радиуса а: , или . При этом и фокусы эллипса как бы сливаются в одной точке - центре окружности. Эксцентриситет окружности равен нулю:
Связь между эллипсом и окружностью может быть установлена и с другой точки зрения. Покажем, что эллипс с полуосями а и b можно рассматривать как проекцию окружности радиуса а.
Рассмотрим две плоскости Р и Q, образующие между собой такой угол а, для которого (рис. 46). Построим в плоскости Р систему координат , а в плоскости Q - систему Оху с общим началом координат О и общей осью абсцисс, совпадающей с линией пересечения плоскостей. Рассмотрим в плоскости Р окружность
![]()
с центром в начале координат и радиусом равным а. Пусть -произвольно выбранная точка окружности, - ее проекция на плоскость Q и - проекция точки М на ось Ох. Покажем, что точка лежит на эллипсе с полуосями а и b.
Эллипсом называется геометрическое место точек плоскости, сумма расстояний от каждой из которых до двух заданных точек F_1 , и F_2 есть величина постоянная (2a) , бо́льшая расстояния (2c) между этими заданными точками (рис.3.36,а). Это геометрическое определение выражает фокальное свойство эллипса .
Фокальное свойство эллипса
Точки F_1 , и F_2 называются фокусами эллипса, расстояние между ними 2c=F_1F_2 - фокусным расстоянием, середина O отрезка F_1F_2 - центром эллипса, число 2a - длиной большой оси эллипса (соответственно, число a - большой полуосью эллипса). Отрезки F_1M и F_2M , соединяющие произвольную точку M эллипса с его фокусами, называются фокальными радиусами точки M . Отрезок, соединяющий две точки эллипса, называется хордой эллипса.
Отношение e=\frac{c}{a} называется эксцентриситетом эллипса. Из определения (2a>2c) следует, что 0\leqslant e<1 . При e=0 , т.е. при c=0 , фокусы F_1 и F_2 , а также центр O совпадают, и эллипс является окружностью радиуса a (рис.3.36,6).
Геометрическое определение эллипса , выражающее его фокальное свойство, эквивалентно его аналитическому определению - линии, задаваемой каноническим уравнением эллипса:
Действительно, введем прямоугольную систему координат (рис.3.36,в). Центр O эллипса примем за начало системы координат; прямую, проходящую через фокусы (фокальную ось или первую ось эллипса), примем за ось абсцисс (положительное направление на ней от точки F_1 к точке F_2 ); прямую, перпендикулярную фокальной оси и проходящую через центр эллипса (вторую ось эллипса), примем за ось ординат (направление на оси ординат выбирается так, чтобы прямоугольная система координат Oxy оказалась правой).
Составим уравнение эллипса, пользуясь его геометрическим определением, выражающим фокальное свойство. В выбранной системе координат определяем координаты фокусов F_1(-c,0),~F_2(c,0) . Для произвольной точки M(x,y) , принадлежащей эллипсу, имеем:
\vline\,\overrightarrow{F_1M}\,\vline\,+\vline\,\overrightarrow{F_2M}\,\vline\,=2a.
Записывая это равенство в координатной форме, получаем:
\sqrt{(x+c)^2+y^2}+\sqrt{(x-c)^2+y^2}=2a.
Переносим второй радикал в правую часть, возводим обе части уравнения в квадрат и приводим подобные члены:
(x+c)^2+y^2=4a^2-4a\sqrt{(x-c)^2+y^2}+(x-c)^2+y^2~\Leftrightarrow ~4a\sqrt{(x-c)^2+y^2}=4a^2-4cx.
Разделив на 4, возводим обе части уравнения в квадрат:
A^2(x-c)^2+a^2y^2=a^4-2a^2cx+c^2x^2~\Leftrightarrow~ (a^2-c^2)^2x^2+a^2y^2=a^2(a^2-c^2).
Обозначив b=\sqrt{a^2-c^2}>0 , получаем b^2x^2+a^2y^2=a^2b^2 . Разделив обе части на a^2b^2\ne0 , приходим к каноническому уравнению эллипса:
\frac{x^2}{a^2}+\frac{y^2}{b^2}=1.
Следовательно, выбранная система координат является канонической.
Если фокусы эллипса совпадают, то эллипс представляет собой окружность (рис.3.36,6), поскольку a=b . В этом случае канонической будет любая прямоугольная система координат с началом в точке O\equiv F_1\equiv F_2 , a уравнение x^2+y^2=a^2 является уравнением окружности с центром в точке O и радиусом, равным a .
Проводя рассуждения в обратном порядке, можно показать, что все точки, координаты которых удовлетворяют уравнению (3.49), и только они, принадлежат геометрическому месту точек, называемому эллипсом. Другими словами, аналитическое определение эллипса эквивалентно его геометрическому определению, выражающему фокальное свойство эллипса.
Директориальное свойство эллипса
Директрисами эллипса называются две прямые, проходящие параллельно оси ординат канонической системы координат на одинаковом расстоянии \frac{a^2}{c} от нее. При c=0 , когда эллипс является окружностью, директрис нет (можно считать, что директрисы бесконечно удалены).
Эллипс с эксцентриситетом 0
В самом деле, например, для фокуса F_2 и директрисы d_2 (рис.3.37,6) условие \frac{r_2}{\rho_2}=e можно записать в координатной форме:
\sqrt{(x-c)^2+y^2}=e\cdot\!\left(\frac{a^2}{c}-x\right)
Избавляясь от иррациональности и заменяя e=\frac{c}{a},~a^2-c^2=b^2 , приходим к каноническому уравнению эллипса (3.49). Аналогичные рассуждения можно провести для фокуса F_1 и директрисы d_1\colon\frac{r_1}{\rho_1}=e .
Уравнение эллипса в полярной системе координат
Уравнение эллипса в полярной системе координат F_1r\varphi (рис.3.37,в и 3.37(2)) имеет вид
R=\frac{p}{1-e\cdot\cos\varphi}
где p=\frac{b^2}{a} фокальный параметр эллипса.
В самом деле, выберем в качестве полюса полярной системы координат левый фокус F_1 эллипса, а в качестве полярной оси - луч F_1F_2 (рис.3.37,в). Тогда для произвольной точки M(r,\varphi) , согласно геометрическому определению (фокальному свойству) эллипса, имеем r+MF_2=2a . Выражаем расстояние между точками M(r,\varphi) и F_2(2c,0) (см. пункт 2 замечаний 2.8):
\begin{aligned}F_2M&=\sqrt{(2c)^2+r^2-2\cdot(2c)\cdot r\cos(\varphi-0)}=\\ &=\sqrt{r^2-4\cdot c\cdot r\cdot\cos\varphi+4\cdot c^2}.\end{aligned}
Следовательно, в координатной форме уравнение эллипса F_1M+F_2M=2a имеет вид
R+\sqrt{r^2-4\cdot c\cdot r\cdot\cos\varphi+4\cdot c^2}=2\cdot a.
Уединяем радикал, возводим обе части уравнения в квадрат, делим на 4 и приводим подобные члены:
R^2-4\cdot c\cdot r\cdot\cos\varphi+4\cdot c^2~\Leftrightarrow~a\cdot\!\left(1-\frac{c}{a}\cdot\cos\varphi\right)\!\cdot r=a^2-c^2.
Выражаем полярный радиус r и делаем замену e=\frac{c}{a},~b^2=a^2-c^2,~p=\frac{b^2}{a} :
R=\frac{a^2-c^2}{a\cdot(1-e\cdot\cos\varphi)} \quad \Leftrightarrow \quad r=\frac{b^2}{a\cdot(1-e\cdot\cos\varphi)} \quad \Leftrightarrow \quad r=\frac{p}{1-e\cdot\cos\varphi},
что и требовалось доказать.
Геометрический смысл коэффициентов в уравнении эллипса
Найдем точки пересечения эллипса (см. рис.3.37,а) с координатными осями (вершины зллипса). Подставляя в уравнение y=0 , находим точки пересечения эллипса с осью абсцисс (с фокальной осью): x=\pm a . Следовательно, длина отрезка фокальной оси, заключенного внутри эллипса, равна 2a . Этот отрезок, как отмечено выше, называется большой осью эллипса, а число a - большой полуосью эллипса. Подставляя x=0 , получаем y=\pm b . Следовательно, длина отрезка второй оси эллипса, заключенного внутри эллипса, равна 2b . Этот отрезок называется малой осью эллипса, а число b - малой полуосью эллипса.
Действительно, b=\sqrt{a^2-c^2}\leqslant\sqrt{a^2}=a , причем равенство b=a получается только в случае c=0 , когда эллипс является окружностью. Отношение k=\frac{b}{a}\leqslant1 называется коэффициентом сжатия эллипса.
Замечания 3.9
1. Прямые x=\pm a,~y=\pm b ограничивают на координатной плоскости основной прямоугольник, внутри которого находится эллипс (см. рис.3.37,а).
2. Эллипс можно определить, как геометрическое место точек, получаемое в результате сжатия окружности к ее диаметру.
Действительно, пусть в прямоугольной системе координат Oxy
уравнение окружности имеет вид x^2+y^2=a^2
. При сжатии к оси абсцисс с коэффициентом 0 \begin{cases}x"=x,\\y"=k\cdot y.\end{cases}
Подставляя в уравнение окружности x=x"
и y=\frac{1}{k}y"
, получаем уравнение для координат образа M"(x",y")
точки M(x,y)
: (x")^2+{\left(\frac{1}{k}\cdot y"\right)\!}^2=a^2 \quad \Leftrightarrow \quad \frac{(x")^2}{a^2}+\frac{(y")^2}{k^2\cdot a^2}=1 \quad \Leftrightarrow \quad \frac{(x")^2}{a^2}+\frac{(y")^2}{b^2}=1,
поскольку b=k\cdot a
. Это каноническое уравнение эллипса. 3.
Координатные оси (канонической системы координат) являются осями симметрии эллипса (называются главными осями эллипса), а его центр - центром симметрии. Действительно, если точка M(x,y)
принадлежит эллипсу . то и точки M"(x,-y)
и M""(-x,y)
, симметричные точке M
относительно координатных осей, также принадлежат тому же эллипсу. 4.
Из уравнения эллипса в полярной системе координат r=\frac{p}{1-e\cos\varphi}
(см. рис.3.37,в), выясняется геометрический смысл фокального параметра - это половина длины хорды эллипса, проходящей через его фокус перпендикулярно фокальной оси ( r=p
при \varphi=\frac{\pi}{2}
). 5.
Эксцентриситет e
характеризует форму эллипса, а именно отличие эллипса от окружности. Чем больше e
, тем эллипс более вытянут, а чем ближе e
к нулю, тем ближе эллипс к окружности (рис.3.38,а). Действительно, учитывая, что e=\frac{c}{a}
и c^2=a^2-b^2
, получаем E^2=\frac{c^2}{a^2}=\frac{a^2-b^2}{a^2}=1-{\left(\frac{a}{b}\right)\!}^2=1-k^2,
где k
- коэффициент сжатия эллипса, 0 6.
Уравнение \frac{x^2}{a^2}+\frac{y^2}{b^2}=1
при a
7.
Уравнение \frac{(x-x_0)^2}{a^2}+\frac{(y-y_0)^2}{b^2}=1,~a\geqslant b
определяет эллипс с центром в точке O"(x_0,y_0)
, оси которого параллельны координатным осям (рис.3.38,в). Это уравнение сводится к каноническому при помощи параллельного переноса (3.36). При a=b=R
уравнение (x-x_0)^2+(y-y_0)^2=R^2
описывает окружность радиуса R
с центром в точке O"(x_0,y_0)
. Параметрическое уравнение эллипса
в канонической системе координат имеет вид \begin{cases}x=a\cdot\cos{t},\\ y=b\cdot\sin{t},\end{cases}0\leqslant t<2\pi.
Действительно, подставляя эти выражения в уравнение (3.49), приходим к основному тригонометрическому тождеству \cos^2t+\sin^2t=1
. Пример 3.20.
Изобразить эллипс \frac{x^2}{2^2}+\frac{y^2}{1^2}=1
в канонической системе координат Oxy
. Найти полуоси, фокусное расстояние, эксцентриситет, коэффициент сжатия, фокальный параметр, уравнения директрис. Решение.
Сравнивая заданное уравнение с каноническим, определяем полуоси: a=2
- большая полуось, b=1
- малая полуось эллипса. Строим основной прямоугольник со сторонами 2a=4,~2b=2
с центром в начале координат (рис.3.39). Учитывая симметричность эллипса, вписываем его в основной прямоугольник. При необходимости определяем координаты некоторых точек эллипса. Например, подставляя x=1
в уравнение эллипса, получаем \frac{1^2}{2^2}+\frac{y^2}{1^2}=1 \quad \Leftrightarrow \quad y^2=\frac{3}{4} \quad \Leftrightarrow \quad y=\pm\frac{\sqrt{3}}{2}.
Следовательно, точки с координатами \left(1;\,\frac{\sqrt{3}}{2}\right)\!,~\left(1;\,-\frac{\sqrt{3}}{2}\right)
- принадлежат эллипсу. Вычисляем коэффициент сжатия k=\frac{b}{a}=\frac{1}{2}
; фокусное расстояние 2c=2\sqrt{a^2-b^2}=2\sqrt{2^2-1^2}=2\sqrt{3}
; эксцентриситет e=\frac{c}{a}=\frac{\sqrt{3}}{2}
; фокальный параметр p=\frac{b^2}{a}=\frac{1^2}{2}=\frac{1}{2}
. Составляем уравнения директрис: x=\pm\frac{a^2}{c}~\Leftrightarrow~x=\pm\frac{4}{\sqrt{3}}
. Кривыми второго порядка
на плоскости называются линии,
определяемые уравнениями, в которых переменные координаты x
и y
содержатся во второй степени. К ним относятся эллипс, гипербола и парабола. Общий вид уравнения кривой второго порядка следующий: где A, B, C, D, E, F
- числа и хотя бы один из коэффициентов A, B, C
не равен нулю. При решении задач с кривыми второго порядка чаще всего рассматриваются
канонические уравнения эллипса, гиперболы и параболы. К ним легко перейти от общих уравнений,
этому будет посвящён пример 1 задач с эллипсами. Определение эллипса.
Эллипсом называется множество
всех точек плоскости, таких, для которых сумма расстояний до точек, называемых фокусами,
есть величина постоянная и бОльшая, чем расстояние между фокусами. Фокусы обозначены как и
на рисунке ниже. Каноническое уравнение эллипса имеет вид: где a
и b
(a
> b
) - длины
полуосей, т. е. половины длин отрезков, отсекаемых эллипсом на осях координат. Прямая, проходящая через фокусы эллипса, является его осью симметрии.
Другой осью симметрии эллипса является прямая, проходящая через середину отрезка
перпендикулярно этому отрезку. Точка О
пересечения этих прямых служит центром
симметрии эллипса или просто центром эллипса. Ось абсцисс эллипс пересекает в точках (a
, О
) и
(- a
, О
), а ось ординат - в точках (b
, О
) и
(- b
, О
). Эти четыре точки называются вершинами эллипса. Отрезок
между вершинами эллипса на оси абсцисс называется его большой осью, а на оси ординат -
малой осью. Их отрезки от вершины до центра эллипса называются полуосями. Если a
= b
,
то уравнение эллипса принимает вид .
Это уравнение окружности радиуса a
, а
окружность - частный случай эллипса. Эллипс можно получить из окружности
радиуса a
, если сжать её в a
/b
раз вдоль оси Oy
. Пример 1.
Проверить, является ли линия, заданная
общим уравнением Решение. Производим преобразования общего уравнения. Применяем перенос
свободного члена в правую часть, почленное деление уравнения на одно и то же число и
сокращение дробей: Ответ. Полученное в результате преобразований уравнение является
каноническим уравнением эллипса. Следовательно, данная линия - эллипс. Пример 2.
Составить каноническое уравнение эллипса,
если его полуоси соответственно равны 5 и 4. Решение. Смотрим на формулу канонического уравения эллипса и подставляем:
бОльшая полуось - это a
= 5
, меньшая полуось -
это b
= 4
. Получаем каноническое уравнение
эллипса: Точки и
, обозначенные зелёным на большей оси, где называются фокусами
. называется эксцентриситетом
эллипса. Отношение b
/a
характеризует "сплюснутость" эллипса.
Чем меньше это отношение, тем сильнее эллипс вытянут вдоль большой оси. Однако степень
вытянутости эллипса чаще принято выражать через эксцентриситет, формула которого приведена
выше. Для разных эллипсов эксцентриситет меняется в пределах от 0 до 1, оставаясь всегда
меньше единицы. Пример 3.
Составить каноническое уравнение эллипса,
если расстояние между фокусами равно 8 и бОльшая ось равна 10. Решение. Делаем несложные умозаключения: Если бОльшая ось равна 10, то её половина, т. е. полуось
a
= 5
, Если расстояние между фокусами равно 8, то число c
из
координат фокусов равно 4. Подставляем и вычисляем: Результат - каноническое уравнение эллипса: Пример 4.
Составить каноническое уравнение эллипса,
если его бОльшая ось равна 26 и эксцентриситет . Решение. Как следует и из размера большей оси, и из уравнения
эксцентриситета, бОльшая полуось эллипса a
= 13
.
Из уравнения эсцентриситета выражаем число c
, нужное для вычисления длины меньшей
полуоси: Вычисляем квадрат длины меньшей полуоси: Составляем каноническое уравнение эллипса: Пример 5.
Определить фокусы эллипса, заданного
каноническим уравнением . Решение. Следует найти число c
, определяющее первые
координаты фокусов эллипса: Получаем фокусы эллипса: Пример 6.
Фокусы эллипса расположены на оси Ox
симметрично
относительно начала координат. Составить каноническое уравнение эллипса, если: 1) расстояние между фокусами 30, а большая ось 34 2) малая ось 24, а один из фокусов находится в точке (-5; 0) 3) эксцентриситет
, а один из
фокусов находится в точке (6; 0) Если -
произвольная точка эллипса (на чертеже обозначена зелёным в верхней правой части эллипса) и
-
расстояния до этой точки от фокусов , то
формулы для расстояний - следующие: Для каждой точки, принадлежащей эллипсу, сумма расстояний от фокусов
есть величина постоянная, равная 2a
. Прямые, определяемые уравнениями называются директрисами
эллипса (на чертеже - красные линии
по краям). Из двух вышеприведённых уравнений следует, что для любой точки эллипса где и -
расстояния этой точки до директрис и
. Пример 7.
Дан эллипс .
Составить уравнение его директрис. Решение. Смотрим в уравнение директрис и обнаруживаем, что требуется
найти эксцентриситет эллипса, т. е. .
Все данные для этого есть. Вычисляем: Получаем уравнение директрис эллипса: Пример 8.
Составить каноническое уравнение
эллипса, если его фокусами являются точки ,
а директрисами являются прямые .Параметрическое уравнение эллипса
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Эллипс, заданный каноническим уравнением

![]() ,
эллипсом.
,
эллипсом.
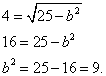
![]() .
.
![]() .
.![]()
Продолжаем решать задачи на эллипс вместе
![]() ,
, .
.![]()







